To view this content, you need to install Java from java.com

CS1050, Spring 2006, Project 9
Graphs
by Jacob Bolton   Email:
Submitted: April 10, 2006

To Load a graph: click in the graphic window and press "l".
To add an edge: click the start point and drag to the end point
These will be snapped to existing points if close enough.
To move a point, click and drag it while pressing the space bar
To toggle the display of point numbers: press "n"
To resize and recenter: press "f"

When run locally in Processing
To save the graph: press "s"
To make a picture: press "i"

When my algorithm is run against the sample points and edges from the project slides it produces the following images and point/vertex coloring data:

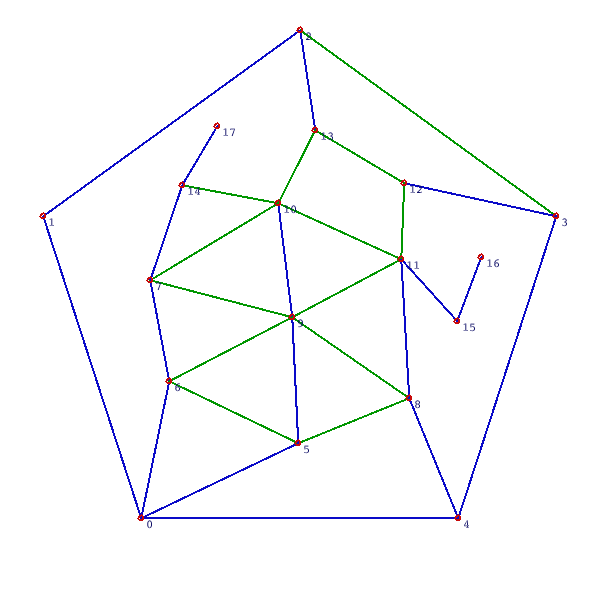
18 vertices
col[0]=1 (141.0,518.0)
col[1]=1 (43.0,216.0)
col[2]=2 (300.0,30.0)
col[3]=2 (556.0,216.0)
col[4]=1 (458.0,518.0)
col[5]=1 (298.0,443.0)
col[6]=1 (169.0,381.0)
col[7]=2 (150.0,280.0)
col[8]=2 (409.0,398.0)
col[9]=2 (292.0,317.0)
col[10]=3 (278.0,203.0)
col[11]=3 (401.0,259.0)
col[12]=3 (404.0,183.0)
col[13]=3 (315.0,130.0)
col[14]=3 (182.0,185.0)
col[15]=4 (457.0,321.0)
col[16]=5 (481.0,257.0)
col[17]=4 (217.0,126.0)

30 edges
col[0]=1 (0,1)
col[1]=1 (1,2)
col[2]=0 (2,3)
col[3]=1 (3,4)
col[4]=1 (4,0)
col[5]=1 (0,5)
col[6]=1 (6,0)
col[7]=0 (6,5)
col[8]=1 (7,6)
col[9]=0 (8,5)
col[10]=0 (6,9)
col[11]=1 (5,9)
col[12]=1 (8,4)
col[13]=0 (7,9)
col[14]=0 (8,9)
col[15]=2 (9,10)
col[16]=0 (10,7)
col[17]=0 (9,11)
col[18]=0 (10,11)
col[19]=2 (11,8)
col[20]=0 (11,12)
col[21]=2 (12,3)
col[22]=2 (2,13)
col[23]=0 (13,12)
col[24]=0 (13,10)
col[25]=0 (10,14)
col[26]=3 (11,15)
col[27]=4 (15,16)
col[28]=3 (14,17)
col[29]=2 (14,7)

The following is the code for the algorithm that produced this: 
//*************************************************************
// **** COMPUTE THE VERTEX SPANNING TREE WITH ROOT AT VERTEX 0
//*************************************************************
// computes the vertex spanning tree (sets colors of edges and points in the tree)
void VST() {
int currentVert = 0;  //set the current vertex to the root
int nextVert = -1;    //don't have a next vertex yet

Vector nextVerts = new Vector();  //prepare a vector for storing the set of next points
Vector newNextVerts = null;       //prepare space for a vector for the following set of points

for (int i = 0; i < vn; i++) colVert[i]=0;  // resets vertex colors to 0 (not visited)
for (int i = 0; i < en; i++) colEdge[i]=0;  // resets edge colors to 0 (not in the VST)
colVert[0]=1;                               // seeds the VST root at vertex 0 (color = 1)

//initialize the set of unvisited verts coming off of the root
for(int i = 0; i < en; i++){
nextVert = -1;  //haven't found an unvisited vert yet
//if an edge starts or ends with the root vert, use the other vert as the next
if(E[i].s == currentVert){
nextVert = E[i].e;
} 
else if(E[i].e == currentVert){
nextVert = E[i].s;
}
//if a vert was determined to be next AND it hasn't been visited
if((nextVert > -1)  && (colVert[nextVert] == 0)){
//set vert and edge distance from root
colEdge[i] = 1;
colVert[nextVert] = 1;
//add this vert to the set of verts to consider next iteration
nextVerts.add(new Integer(nextVert));
}
}

//process the set of next verts until there are no more next verts detected
while(nextVerts.size() > 0) {
newNextVerts = new Vector();  //create an empty set of vertices to follow this set
for(int i = 0; i < nextVerts.size(); i++) {  //for each vertex in the current set
//get the vertex number
currentVert = ((Integer)nextVerts.elementAt(i)).intValue();
//initialize the set of unvisited verts coming off of the current vertex
for(int j = 0; j < en; j++){
nextVert = -1;  //haven't found an unvisited vert yet
//if an edge starts or ends with the current vert, use the other vert as the next
if(E[j].s == currentVert){
nextVert = E[j].e;
} 
else if(E[j].e == currentVert){
nextVert = E[j].s;
}
//if a vert was determined to be next AND it hasn't been visited
if((nextVert > -1)  && (colVert[nextVert] == 0)){
//set vert and edge distance from root
colEdge[j] = colVert[currentVert];  //next edges are then same distance as the starting vert
colVert[nextVert] = colVert[currentVert] + 1;  //next verts are 1 farther than previous
//add this vert to the set of verts to consider next iteration
newNextVerts.add(new Integer(nextVert));
}
}
}
//switch to the newly formed set of verts to follow
nextVerts = newNextVerts;
}
}

To discuss the time complexity, V will stand for the number of vertices and E will stand for the number of edges. Here is a breakdown of the operational loops: From this we can see that the worst case complexity is $V + 2E + ABE$; however, we have not yet defined $A$ and $B$. The worst case value for $A$ is if you always have only one vertex in a set at a time (the graph would be a simple path). Thus, $A = V - 1$ since the root vertex has already been accounted for. The worst case value of $B$ occurs when a vertex is connected to as many other vertices as possible making $B = V - 1$ since the root vertex has already been accounted for. This means that $V + 2E + ABE = E(V - 1)^2 + 2E + V = EV^2 - 2EV + V + 3E$. Now that we have the expression we will reduce it appropriately for the final worst-case complexity. Starting with the $V$ terms, we drop the lesser orders leaving our expression as $O(EV^2 + 3E)$. Now when reducing the $E$ terms we can state $O(EV^2 + 3E) = O(EV^2 + E)$ and furthermore $O(EV^2 + E) = O(EV^2)$. This is because when $E \ge 1$, $V \ge 2$. So $EV^2 \ge E$ making the worst-case complexity $O(EV^2)$.

LaTeX source for equations.

Source code: P9 pv2D

Built with Processing